计算投资组合的风险系数

一般来说，金融资产的投资回报率是与它的波动风险成正比的。比如银行CD定存账户的波动风险为零，它的回报率很低；股票的波动风险比较高，所以长期投资股票的回报率要比银行CD定存的要高。

一个理性的投资者应当追求的是冒尽可能小的风险来换取大的回报，换一种说法就是，在能够承受的波动风险下获得最大的报酬，或者在相同报酬的情况下去冒尽可能低的波动风险。

1990年度的诺贝尔经济学奖得主威廉·夏普（William Sharpe）提出了著名的夏普比率(Sharpe Ratio)，夏普比率衡量的是在相同的波动风险情况下、不同的金融资产或投资组合的回报率。哪个金融资产或投资组合的夏普比率越高，它就越值得投资。

假设一个投资组合的长期平均年回报率是12%，而联邦债券的长期平均年利率是3%，投资组合的波动风险标准偏差是6%，那么夏普比率的计算公式是：（12% - 3%）/ 6% = 1.5
这表示如果投资者所冒的波动风险增加1%，换来的是1.5%的多余回报。

下面用我的“ETF基金投资组合”为例，实际计算一下这个投资组合的夏普比率(Sharpe Ratio)。

从2003年至今，ETF基金投资组合的资金成长曲线如下：



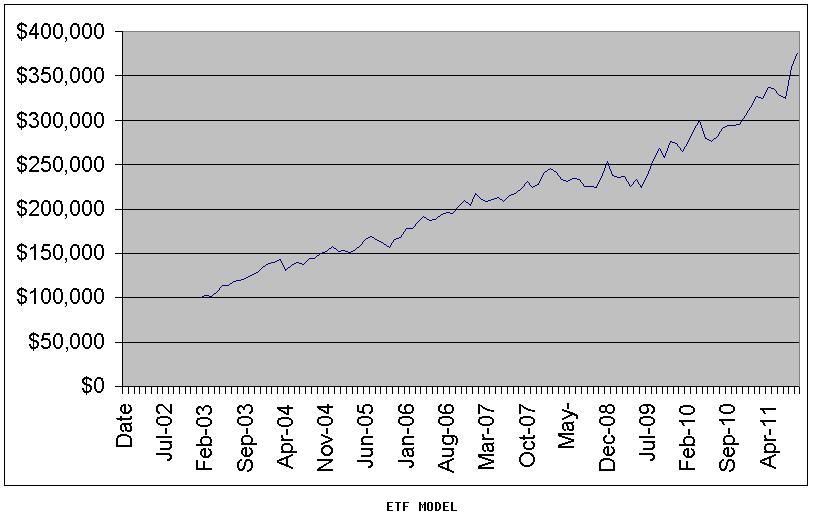
ETF基金量化投资组合的主要参数是：

起始投资金额：10万美元
投资工具：主要金融资产的ETF基金
年均收益率：16.5%
年均交易次数：4.4次 （大约每个季度交易1次）
最大浮亏程度：11.4%

每个月利润或亏损的分布情况如下：



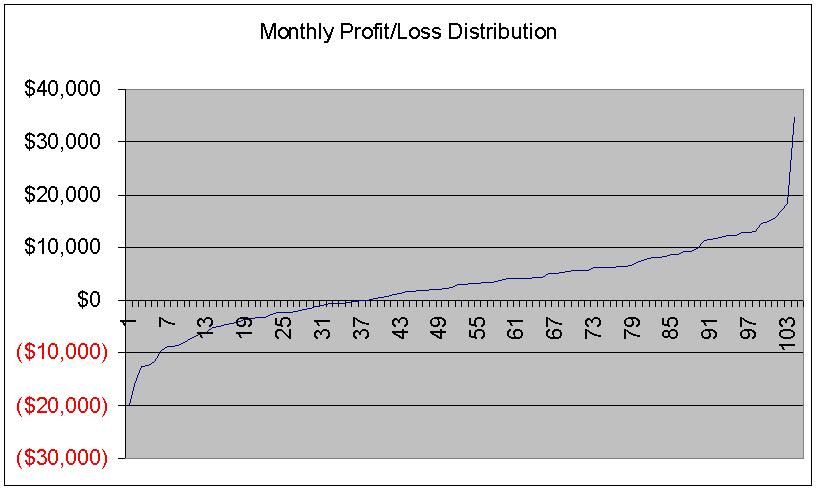
从图中可见，在总共104个月中，有66个月赚钱，其余38个月亏损；最大单月利润34861美元，最大单月亏损20041美元。

同样用起始投资金额10万美元购买标普500指数的资金成长曲线如下：



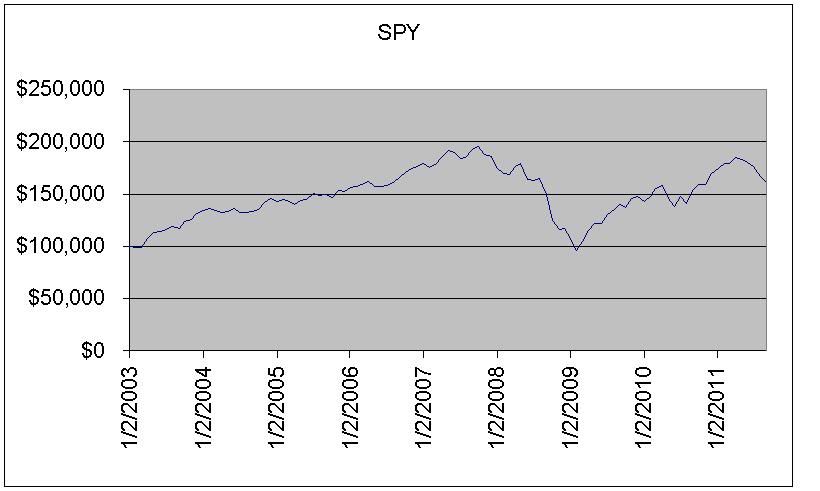
从2003年至今的104个月中，ETF基金投资组合的回报率为372%，标普500指数的回报率为161%，每个月ETF基金投资组合超过标普500指数回报金额的波动风险标准偏差是88%，所以ETF基金投资组合的夏普比率(Sharpe Ratio)是：

（372% - 161%）/ 88% = 2.4

这表示如果ETF基金投资组合的波动风险增加1%，换来的是2.4%的多余回报。ETF基金投资组合的夏普比率2.4是一个非常令人满意的风险回报系数。

=========

欢迎访问我的博客：

依据事实数字，把握市场脉搏，运筹金融世界。

http://murmuronhudson.blogspot.com/

我在文学城的群组